בואו נדבר על משחקים. רובנו אוהבים לשחק משחקים בעלי אופי מאוד מגוון – שש בש, פיפ"א, פוקר,כדורגל ועוד משחקים רבים. לעתים נשאלת השאלה האם קיימת אסטרטגיה שתעלה את סיכוי הנוקט בה לנצח? ברור שהתשובה היא – תלוי. במה תלוי? באופי המשחק. לדוגמא – האם יש אסטרטגיה שאם נבחר בה נוכל להעלות את הסיכוי שלנו לנחש תוצאה של הטלת מטבע? מכיוון שהסיכוי לכל תוצאה הוא 50% התשובה היא לא. לעומת זאת – קיימים מצבים בהם דווקא קיימת אסטרטגיה כזו. את המצבים הללו ניתן לסווג לסוגים שונים ועל חלק קטן מאוד מהם נדבר בהמשך.
אבל למה זה חשוב לנו? כי ענפי ספורט הם משחקים ואם נוכל (לא נוכל) לבחור אסטרטגיות שיעזרו לנו לנצח, נוכל לשפר את ביצועי הקבוצה שלנו (או השחקן במידה ומדובר בספורט יחידני). מבלי להיכנס לתוך המתמטיקה, רק אומר שלא מעט מהחוקרים הבכירים בעולם תורת המשחקים יקראו לנסיונות להשתמש בה כדי לפתור דילמות אמיתיות שרלטנות, אבל חברות לניתוח נתונים עושות מהשיטות הללו הון עתק אז כל עוד קיימים פראיירים שישלמו, למי אכפת?
לפני שנתחיל, אני חייב להפריך מיתוס לטובת כל צופי הסרט "נפלאות התבונה" – ג'ון נאש לא המציא את תורת המשחקים. אחרי שהורדנו את זה, בואו נתחיל מהיסוד. מהו משחק?
בשפה חופשית ועבור הצורך שלנו, אנחנו נגדיר משחק כמצב שבו משתתף אחד או יותר נדרשים לקבל החלטה אשר יכולה לייצר להם תועלת בהמשך. כדי להבהיר את ההיגיון, נדגיש שמשחק יכול להיות משחק יחיד או מרובה משתתפים, הוא יכול להיות משחק שבו המטרות של המשתתפים מנוגדות (למשל שח-מט) או משותפות, הוא יכול לכלול מצב שבו לא כל האינפורציה גלויה (למשל משחק הטבעת צוללות) ואפילו יכול לאפשר מצב שבו התועלת לכל משתתף שונה בכל מצב (למשל: במשחק החוץ הקרוב של מנצ'סטר סיטי מול ריאל מדריד בליגת האלופות שער חוץ של סיטי שווה הרבה יותר משער בית של ריאל מכיוון שתוצאה כגון 1:1 מעלה את סיטי לגמר. במקרה זה, למרות שלא ניצחה במשחק הכדורגל עצמו, סיטי מנצחת במשחק שהוא העימות על העלייה לגמר).
סוג נוסף ונפוץ מאוד של משחקים נקרא משחק סכום אפס. בסוג משחק זה, ניצחון של צד אחד משמעו בהכרח הפסד של הצד השני (במקרה של משחק עם שני משתתפים). דוגמאות למשחקים סכום אפס הם למשל משחק כדורסל, בו אין אפשרות לשויון. דוגמא נוספת מתחום אחר היא למשל עימות בין טילים – טיל מיירט מנסה ליירט טיל תוקף. יירוט משמעו ניצחון למיירט ופספוס מהווה ניצחון לתוקף. גמר ליגת האלופות הוא דוגמא חריגה למשחק סכום אפס מכיוון שבכלליות כדורגל אינו משחק סכום אפס שהרי הוא מאפשר תוצאת תיקו בסיום המשחק.
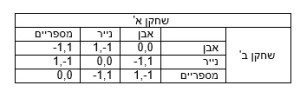
מושג נוסף וחשוב הוא שיווי משקל. שיווי משקל בתורת המשחקים הוא מושג מעט מסובך וקיימים עבורו מספר סוגים, אך אנחנו נשתמש בניסוח פשוט ופרימיטיבי (גם אם מעט פחות מדויק) המגדיר שיווי משקל כ"מצב שבו אף אחד מהשחקנים לא ירצה לשנות את האסטרטגיה שלו". פישוט יחסית קל להבנה של משחק עושה שימוש בטבלת רווח. טבלה זו מתארת את המצבים השונים ואת הרווח/הפסד של כל שחקן בכל אחד מהם. כדי להמחיש נשתמש במשחק אבן נייר מספריים.
הסכום בכל תא מייצג את התועלת הכללית, כאשר המספר השמאלי מייצג את התועלת של שחקן א' והמספר הימני מייצג את התועלת של שחקן ב'. למשל: אם שחקן א' בוחר מספריים ושחקן ב' בוחר נייר, התועלת לשחקן א' היא 1 (ניצחון) והתועלת לשחקן ב' היא 1- (הפסד), סה"כ התועלת היא 0 תמיד ולכן זהו משחק סכום אפס. חשוב לשים לב שלא משנה על איזה מצב נסתכל תמיד יהיה לפחות שחקן אחד שירצה לשנות את הבחירה שלו כי תהיה לו (לפחות) בחירה אחת שתוביל ליותר תועלת עבורו ולכן זהו משחק ללא שיווי משקל (תחת ההנחה כי לא ניתן לבחור אסטרטגיה מעורבת – כלומר לא ניתן לבחור אסטרטגיה בסגנון של: "בהסתברות של 30% אבחר כך ובהסתברות של 70% אבחר אחרת – נחזור למושג האסטרטגיה המעורבת בהמשך).
אז במידה ואבן, נייר ומספריים לא מספיק ספורט עבורכם עולה כעת השאלה: "יופי, חפרת חפרת, אבל איך זה קשור לספורט??". אז הנה דוגמא מאוד פשוטה.
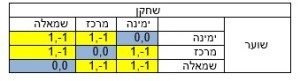
הסיטואציה: בעיטת פנדל. לצורך ההפשטה שתעזור לנו להימנע מהמון מתמטיקה ותאפשר הדגמת העיקרון, נניח המון הנחות מקלות שאפרט בסוף, אך בגדול המצב הוא שחקן מול שוער, השחקן יכול לבחור לבעוט שמאלה, ימינה או למרכז. השוער יכול לבחור לזנק שמאלה, ימינה או למרכז. השחקן לעולם אינו מחטיא את המסגרת, במידה והשוער מזנק לכיוון הנכון הוא תמיד עוצר את הכדור. אין השפעות פסיכולוגיות חיצוניות כגון: משחק בית/חוץ, קהל עוין/תומך, שוער קופץ מצד לצד כמו חולה פרקינסון ועושה פרצופים של ליצן.
המספר שמאלי הוא תועלת השחקן והימני הוא תועלת השוער. הדבר הראשון אליו נשים לב הוא שזהו אינו משחק סימטרי – בשישה מתוך תשעת המצבים האפשריים השחקן גובר על השוער. זה כמובן צריך להיות הגיוני עבורכם מכיוון שזה אכן תואם את האינטואיציה שלכם שקל הרבה יותר להבקיע פנדל מאשר לעצור אחד. בנוסף, השוער לא יכול "לנצח" את הבועט אלא רק למנוע מהבועט לנצח ולכן השוער נמצא בעמדת נחיתות. אז השאלה הבאה היא מהי האסטרטגיה המנצחת עבור הבועט/שוער? הדרך למצוא אחת כזו (לצורך הדוגמא עבור הבועט) היא למצוא אסטרטגיה כזו כך שבכל מצב תועלת השוער תהיה זהה. אם הבועט יכול למצוא אסטרטגיה כזו אזי השוער לא ידע לאן לקפוץ מכיוון ששום תנועה לא תוביל לעליית התועלת שלו. עבור המצב הנוכחי אפשר להיעזר בהגיון במקום במתמטיקה ולראות שהאסטרטגיה המנצחת עבור הבועט היא לבעוט בהסתברות שווה לכל כיוון כלומר – בהסתברות שליש למרכז, בהסתברות שליש ימינה ובהסתברות שליש שמאלה. אם זה לא הגיוני לכם חישבו על הסיטואציה הבאה – אם השוער יבחר להיות תמיד במרכז הוא יעצור שליש מהכדורים , אם יבחר ללכת תמיד ימינה גם כן יעצור שליש מהכדורים וכנ"ל לגבי בחירה לזנק שמאלה. כלומר לא משנה מה הבחירה שלו, תועלתו קבועה.
כאן הזמן לעצור רגע ולהבין את המורכבות האמיתית של תורת המשחקים וההנחות שצריך להניח בכדי לחשב אסטרטגיות מנצחות. ברור כי האסטרטגיה המנצחת תלויה באופן שבו מציגים את המשחק – כלומר עבור מצב אמיתי ולא סינטטי כמו שהראיתי למעלה. חשוב ביותר לבנות מודל מדויק ככל שניתן של הסיטואציה וזו כבר עבודה קשה מאוד מהרבה סיבות ובינהן למשל:
אין שוער מושלם בעולם, גם זינוק למקום הנכון לא מבטיח עצירת פנדל.
אין שחקן מושלם בעולם – לפעמים שחקנים מחטיאים את המסגרת.
יש הרבה יותר אפשרויות בעיטה וזינוק מאשר שמאלה/ימינה/מרכז.
כל שחקן הוא שונה – שחקנים מסוימים בועטים שמאלה טוב יותר מאשר ימינה (מבחינת עוצמה,דיוק וכו') וכנ"ל לגבי שוערים.
בקיצור – אין סוף לכמות המידע שצריך לאסוף על מנת לייצר מודל מדויק של המשחק. אם זה לא מספיק, אז גם צריך לקחת בחשבון שכל החלפה של אחד מהשחקנים משנה את המודל לחלוטין (לדוגמא: רונאלדו מול צ'ך זהו מודל שונה לחלוטין מברדה מול ראיקוביץ'). מסיבה זו חוקרי תורת המשחקים מלגלגים על הנסיון להחיל את תוצאות מחקריהם על סיטואציות אמיתיות בצורה שתנבא אסטרטגיות מנצחות בהצלחה.
עם זאת, מי שלא מלגלג על כך הן חברות ניתוח המידע. לחברות אלו לא אכפת מאיכות המידול המתמטי. הן משתמשות במודלים סטטיסטיים בכדי לשערך את התועלת של הלקוחות שלהם במצבים שונים במשחק, למשל באופן הבא: במשחק של ריאל מול מנצ'סטר סיטי, יתכן שרונאלדו יבעט פנדל מול הארט. בהנחה והוא לא עשה זאת בעבר מספיק פעמים בכדי לייצר סטטיסטיקה משמעותית על סיכויי ההצלחה והכשלון שלו מולו, האנליסטים של סיטי בודקים את כל בעיטות הפנדל של רונאלדו (נניח בשלוש השנים האחרונות) ורואים האם יש לו כיוון מועדף, האם כאשר השוער מזנק לכיוון הנכון הוא מצליח לקלוט את הכדור וכו' ובונים מודל כללי של רונאלדו בפנדל. המודל אינו שלם כי אינו לוקח בחשבון את השוער הספציפי של סיטי, אך זה הכי טוב שניתן לבנות. על סמך המודל הזה האנליסטים בונים עבור הארט אסטרטגיה "מנצחת" במובן מסוים. את אותו הדבר עושים במדריד, כמובן תחת ההנחה שהארט מתכונן לרונאלדו. בסופו של דבר זה מסתכם בפתקים עם הוראות לשוער/בועט.
מכיוון שהמודלים הללו אינם מושלמים, קשה מאוד לנבא את מידת ההצלחה של האסטרטגיות הללו במיוחד כאשר השחקנים רשאים לפעול באופן אקראי ומכאן לעתים נובעת האשמת השרלטנות. עם זאת, היום בעידן ה"צ'יפים שמיפים", קל מאוד לחברות לאסוף המון מידע בעלות אפסית. מידע זה שנאסף באימונים ובמשחקים מאפשר בנייה של מודלים מתמטים די מדויקים לניבוי יכולות של שחקנים ואף תוצאות של סיטואציות במשחקים.
הנקודה החלשה ביותר של ניתוח משחקים בצורה שהוסברה כאן היא שאחת ההנחות היסודיות היא ששני השחקנים פועלים באופן הגיוני כלומר – למקסם את התועלת של עצמם. זו הסיבה שלעתים אסטרטגיות שנראות במבט ראשון תמוהות מנצחות אסטרטגיות מבוססות תורת המשחקים. הרי בעולם שבו אסטרטגיה מנצחת תמיד תוביל לניצחון ושחקן טוב תמיד מנצח שחקן פחות טוב, לא היינו רואים את לסטר מניפים את צלחת האליפות ואת דונאלד טראמפ דוהר לבית הלבן…
לכן, בעוד אנליסטים וסטטיסטיקאים תולשים שערות מראשיהם ומאבדים שעות שינה בכדי לפתח מודלים שיחזו תופעות כמו לסטר, אנחנו יושבים מול הטלויזיה ונהנים מהכאוס. אז מה אתם אומרים?
? Wanna Play a Game